Kombinatorische Optimierung

Inhalt

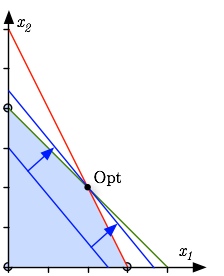Kombinatorische Optimierungsprobleme treten bei vielen praktischen Anwendungen auf (z.B. Flugplanung, Produktionsplanung, Transportplanung, Schichtplanung, Logistik).

Nach einer Einführung in verschiedene kombinatorische Optimierungsprobleme werden allgemeine Optimierungsmethoden (exakte und heuristische Verfahren) vorgestellt und an Beispielen aus der Praxis illustriert. Danach werden kombinatorische Optimierungsprobleme behandelt, die sich als lineare Programme formulieren und effizient mit dem Simplexverfahren lösen lassen.

Stichworte: Branch-and-Bound-Algorithmen, Dynamische Programmierung, Constraint Programming, Heuristiken, Lokale Suche, Tabusuche, Genetische Algorithmen, Ameisenalgorithmen, Approximationsalgorithmen mit Gütegarantie, Lineare Programmierung, Simplexverfahren, Spieltheorie

Literatur

• E.H.L. Aarts, J.K. Lenstra: Local Search in Combinatorial Optimization, Wiley, 1997.
• R.K. Ahuja, T.L. Magnanti, J.B. Orlin: Network Flows, Prentice Hall, 1993.
• P. Brucker, S. Knust: Complex Scheduling, Springer, 2. Auflage, 2012.
• E. Burke, G. Kendall: Search Methodologies: Introductory Tutorials in Optimization and Decision Support Techniques, Springer, 2005.
• V. Chvatal: Linear Programming, W.H. Freeman and Company, 1983.
• J. Dreo, A. Petrowski, P. Siarry, E. Taillard: Metaheuristics for Hard Optimization: Methods and Case Studies, Springer, 2006.
• M. Garey, D.S. Johnson: Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman and Company, 1979.
• M. Gendreau, J.-Y. Potvin: Handbook of Metaheuristics, Springer, 2010.
• F. Glover, G.A. Kochenberger: Handbook of Metaheuristics, Kluwer, Boston, 2003.
• F. Glover, M. Laguna: Tabu Search, Kluwer, Boston, 1997.
• T. Grünert, S. Irnich: Optimierung im Transport, Band I: Grundlagen, Shaker, 2005.
• J. Kallrath: Gemischt-ganzzahlige Optimierung: Modellierung in der Praxis, Springer Spektrum 2013.
• Z. Michalewicz, D.B. Fogel: How to Solve It: Modern Heuristics, Springer, 2004.
• C.H. Papadimitriou, K. Steiglitz: Combinatorial Optimization, Prentice Hall, Englewood Cliffs, N.J., 1982.
• C.R. Reeves: Modern Heuristic Techniques for Combinatorial Problems, Blackwell Scientific Publications, 1993.
• E. Tsang: Foundations of Constraint Satisfaction, Academic Press,1993.
• R. Vanderbei: Linear Programming, Foundations and Extensions, Springer, 2001.

Materialien

• Skript
• Überblick
• Folien B&B
• Folien DP
• Folien CP
• Folien Heuristiken
• Folien NP/Approx
• Folien LP

Materialien KO++

• Skript
• Folien VRP
• Folien Sportligaplanung
• Praktische Aufgaben
• paper zu GA TSP
• paper zu VRP
• paper zu coe
• paper zu coe/breaks

Software

• ZIMPL
• SCIP

Zur Lösung von LP- und MIP-Problemen wird in den Übungen die SCIP Optimization Suite eingesetzt, die die Programme ZIMPL, SCIP und SoPlex enthält. Diese sind für den akademischen Einsatz frei verfügbar. Die Programme sind auf den CIP-Pool-Rechnern installiert, können aber auch auf dem eigenen Computer verwendet werden.

Um ZIMPL bzw. SCIP in allen Verzeichnissen ausführen zu können, müssen Sie das Installationsverzeichnis in der PATH Variable hinzufügen. Eine Beschreibung dazu finden Sie z.B. hier

Teilnahme

Die Veranstaltung ist vorgesehen für B.Sc. ab dem 3. Semester. Teilnehmen können alle interessierten Studierenden aus den Studiengängen Informatik, Mathematik, Angewandte Systemwissenschaft und Cognitive Science.

Schein

Vertiefungsmodul KO++